Evaluating Recursion Through Tracing

Tracing can be used to evaluate a recursive method call. In this tutorial, we will explore how to use tracing to methodically interpret any recursive method call.

It is helpful to first identify the base case and the recursive call along with the reduction that is being made to reach the base case.

Computing Exponents and Recursion Example

int power(int base, int exp) {    
   if (exp == 0) 
      return 1;    
   return base * power(base, exp - 1);
}

• What is the base case?
  • exp == 0
  • The recursion will stop when exp equals 0.
• What is the recursive call? How does it progress to the base case?
  • The recursive call is found in the else branch, power(base, exp - 1)
  • The recursive call is part of a return value, base * power(base, exp - 1)
  • The recursive call progresses toward the base case by subtracting 1 from exp each time it is called. Eventually, exp will equal 0.

A tree of calls can be recorded from the first call through to the base case and then fully evaluated once the base case is reached.

The call power(2, 3) returns 8.

Your Turn

Let's try it in the Java Playground.

• Predict the output.
• Run the code to determine if your prediction is correct.
• Experiment with this code.
  • What happens when you change the initial call to power(2, 5)?
  • What happens when you change the initial call to power(3, 2)?
  • What happens when you change the initial call to power(2, 0)?
  • For what values of exp will this method not work as expected?

Fibonacci and Recursion Example

Consider another recursive method example that will have multiple branches.

• Identify both the base case and the recusive call.
• How is the recursive call progressing toward the base case?

int fibonacci(int n) {
    if (n <= 1) {
      return n;
    }
    return fibonacci(n - 1) + fibonacci(n - 2);
}

• What is the base case?
  • n <= 1
  • The recursion will stop when n is less than or equal to 1.
• What is the recursive call? How does it progress to the base case?
  • There are two recursive calls found in the return statement after the if statement.
    • fibonacci(n - 1)
    • fibonacci(n - 2)
  • Both recursive calls progress toward the base case. The first recursive call subtracts 1 from n each time it is called and the second call substracts 2 from n. Eventually, in both calls n will equal 0.

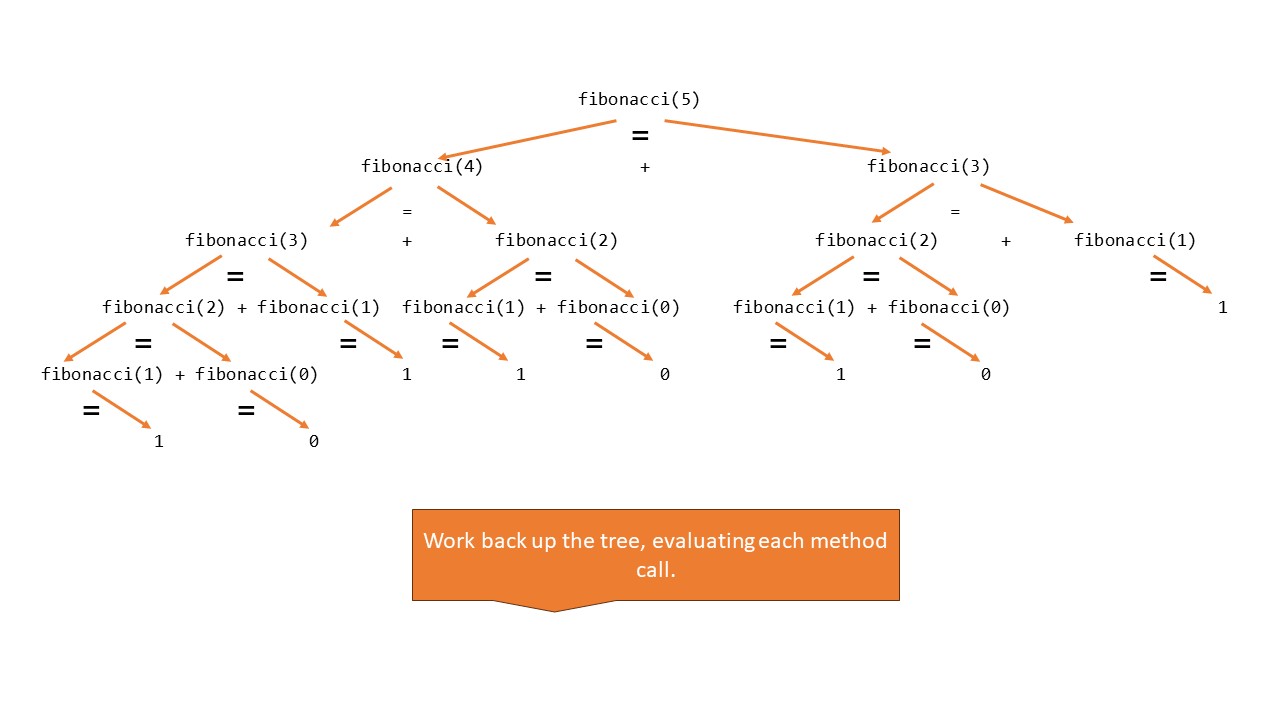
Consider the following tracing of calls for fibonacci(5):

The call fibonacci(5) returns 5.

Your Turn

Let's try it in the Java Playground.

• Predict the output.
• Run the code to determine if your prediction is correct.
• Experiment with this code.
  • What happens when you change the initial call to fibonacci(1)?
  • What happens when you change the initial call to fibonacci(0)?
  • What happens when you change the initial call to fibonacci(10)?
  • Are there values for n that cause this method to not work as expected?

A tree could also be a useful visual when tracing these calls. It might look something like the following:

Complete List of Recursion Tutorials

• Learn: Introduction to Recursion
• Learn: Evaluating Recursive Calls Through Tracing

Resources

• Practice: Evaluate Recursive Calls